对于图G=(V,E),V代表点,E代表边。图有两种标准的表示方法:邻接矩阵法和邻接链表法。
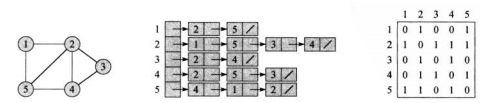
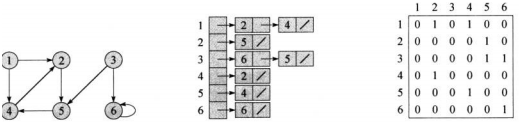
| 邻接链表法适合表示边的条数少的稀疏图,可以节约存储空间。对于有向图G来说,边(u,v)一定会出现在链表Adj[u]中,因此,所有链表的长度之和一定等于 | E | 。对于无向图来说,边(u,v)会同时出现在Adj[u]和Adj[v]中,因此所有链表的长度之和一定等于2 | E | 。但是邻接链表要获取某条边(u,v)的信息必须遍历Adj[u] ,当边数较多时,因为链表过长会增大计算时间。通过在链表结点增加属性可以附带信息,比如边的权重。 |
邻接矩阵法会存在一定的空间冗余,但所有边的信息获取都可以在O(1)的时间完成,效率较高。对于无向图必定是一个对称矩阵,可以用上三角或下三角来压缩存储,而有向图通过行->列的形式来表示方向,可以在矩阵中存储边的权重。
广度优先搜索
广度优先搜索是指,从已发现结点和为发现结点之间的边间沿着广度方向向外扩展,对一个结点k来说,首先探索与他直接相邻的所有结点,然后再去发现其他间接相邻的节点。
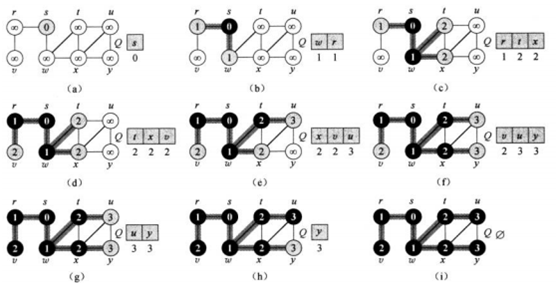
如图的无向单位图白色代表未知的结点,灰色是已知但未探索完周边相邻结点的结点,黑色是已经发现完直接相邻结点的已知结点。要求出从s到所有结点的最短路径长度。(a)开始只有s是已知的将s存入队列。(b)从队列中取出s检查直接相邻的结点有w和r,他们的最短路径长是1,存入队列然后s被标记为黑色。(c)从队列中取出w,检查w直接相邻的未知结点有t和x,路径长度为2,同样入队并将w涂黑。依次出队检测完所有结点之后,可以得到所有点的最短路径长度即(i)所示。代码方面BFS算法通常是借助队列来存储已发现等待进行周边探索的结点。
#include<stdio.h>
#include<queue>
using namespace std;
#define SIZE 10
int G[SIZE][SIZE];//邻接矩阵,参数初始化略
int length[SIZE];//最短路径长度
int known[SIZE];
void bfs (int start){
queue<int> queue;
queue.push(start);
length[start] = 0;
while(queue.size() != 0){
int temp = queue.front();//由于离开始结点近的点一定会先入队,所以算法会按照距离开始结点的顺序进行遍历,即广度优先
queue.pop();
for(int i = 0; i < SIZE; i++){
if(known[i] != 1 && G[i][temp] == 1){
//存在路径且该点未被发现过,标记该点为已知,最短路径长更新为检查结点+1,加入队列
known[i] = 1;
length[i] = 1 + length[temp];
queue.push(i);
}
}
}
}
深度优先搜索
上面提到广度优先搜索是先探索完该结点周边一圈之后,再从这一圈中的某个点开始探索它周边的一圈。深度优先搜索的策略则是,在图中尽可能的深入,顺着一条路径探索直到该结点所有的相邻边都是已被探索过的,然后回到该路径上一个前驱结点继续该过程。由于后探索到的结点会再到达尽头后立刻开始出发探索,所以可以利用栈结构后进先出的特点完成DFS算法,也可以使用递归。
#include<stdio.h>
#include<stack>
using namespace std;
#define SIZE 10
int G[SIZE][SIZE];//邻接矩阵,参数初始化略
int length[SIZE];//最短路径长度,初始化length[start]=0,其他为正无穷
int visit[SIZE];//该结点是否已被访问过
void dfs(int start){
for(int i = 0; i < SIZE; i++){
if(G[start][i] == 1){//选择该结点相邻的路径
if(length[start] + 1 < length[i])
length[i] = length[start] + 1;//检查最小路径是否是最短的
if(visit[i] == 0){
dfs(i);//若该结点为被访问过则对他进行dfs
visit[i] = 1;
}
}
}
}
void dfsQueue(int start){
length[start] = 0;
stack<int> stack;
stack.push(start);
while(stack.size() != 0){
int temp = stack.top();//获取栈顶元素
stack.pop();
for(int i = 0; i < SIZE; i++){
if(G[temp][i] != 0){
length[i] = (length[temp] + 1) < length[i] ? length[temp] + 1 : length[i];
if(visit[i] == 0){
queue.push(i);
visit[i] = 1;//避免同一个点被重复入栈
}
}
}
}
}
拓扑排序
对于一个无环图来说,如果存在边(u,v)则u的拓扑排序在v的前面。实际例子来说,我们必须要先穿袜子再穿鞋子,先穿内衣再穿外套,这就是拓扑排序。
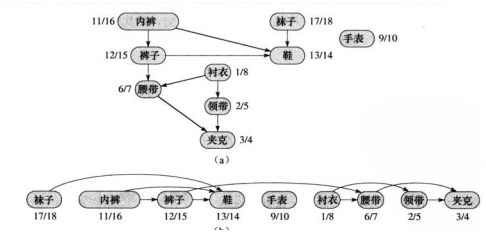
如图所示,将(a)中的拓扑顺序排成(b)中的实际的操作顺序。拓扑排序可以通过DFS来实现,从第一个点到最后一个点,若之前没有被探索过且没有前驱点就调用DFS,所有点被探索的先后次序就是最后的排序。
#include<stdio.h>
#include<vector>
using namespace std;
#define SIZE 10
int G[SIZE][SIZE];//邻接矩阵,参数初始化略
int length[SIZE];//最短路径长度,初始化length[start]=0,其他为正无穷
int visit[SIZE];//该结点是否已被访问过
vector<int> path;//最后的排序结果
void dfs(int start){
path.push_back(start);
for(int i = 0; i < SIZE; i++){
if(G[start][i] == 1){//选择该结点相邻的路径
if(length[start] + 1 < length[i])
length[i] = length[start] + 1;//检查最小路径是否是最短的
if(visit[i] == 0){
dfs(i);//若该结点为被访问过则对他进行dfs
visit[i] = 1;
}
}
}
}
int main(void){
int i,j;
for(i = 0; i < SIZE; i++){
if(visit[i] == 1)
continue;
for(j = 0; j < SIZE; j++){
if(G[j][i] == 1){
break;
}
}
if(j == SIZE){
dfs(i);//只有未被探索过,没有先驱路径的点会在主函数被调用
}
}
return 0;
}
强连通分量
强连通分量是指在有向图中,存在一个最大的结点集合C,对于C中的任意一对结点u和v来说,同时存在路径u→v和v→u,他们之间可以相互到达。这样的集合即为强联通分量。
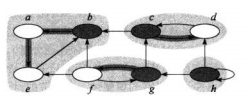
如图所示的阴影部分各自是一个强联通分量。可以通过对图G的每个节点进行DFS获得他能够到达的所有结点,然后对图G进行转置再进行一次每个结点能够到达结点的计算。当且仅当两个结点可以相互到达时他们属于同一个强连通分量。
#include<stdio.h>
using namespace std;
#define SIZE 10
int G[SIZE][SIZE];//邻接矩阵,参数初始化略
int visit[SIZE];//该结点是否已被访问过
int num;//统计连通量个数
int part[2][SIZE];//两次连通量记录
int res[SIZE];//最终结果
void dfs(int start, int time){;
part[time][start] = num;//
for(int i = 0; i < SIZE; i++){
if(G[start][i] == 1){//选择该结点相邻的路径
if(visit[i] == 0){
dfs(i, time);//若该结点未被访问过则对他进行dfs
visit[i] = 1;
}
}
}
}
void init(){
int i;
for(i = 0; i < SIZE; i++)
visit[i] = 0;
num = 0;
}
int main(void){
int i,j, temp;
init();
for(i = 0; i < SIZE; i++){
if(visit[i] == 0){
dfs(i, 0);
num++;
}
}
//图的转置
for(i = 0; i < SIZE; i++){
for(j = i + 1; j < SIZE; j++){
temp = G[i][j];
G[i][j] = G[j][i];
G[j][i] = temp;
}
}
init();
for(i = SIZE - 1; i >= 0; i--){
if(visit[i] == 0){
dfs(i, 1);
num++;
}
}
init();
for(i = 0; i < SIZE; i++){
if(visit[i] == 1)
continue;//已经确认属于某个连通分量的结点跳过下面的查探步骤
res[i] = num++;
for(j = 0; j < SIZE; j++){
if(i != j && part[0][i] == part[0][j] && part[1][i] == part[1][j]){
res[j] = res[i];//若i和j在两图中都属于同个连通量,则他们属于同一个强连通量
visit[j] = 1;
}
}
visit[i] = 1;
}
return 0;
}