红黑树是一棵二叉搜索树,每个结点上增加了一个属性来存储颜色是红色还是黑色,红黑树可以确保没有一条路径会比其他路径长出2倍,所以近似可以认为是平衡的。
每个结点包含5个属性:color, key, left, right, p。如果一个结点没有子结点或者父结点,则该结点的相应指针属性为NIL,这些NIL可以视为树的叶结点,带关键字的结点视为内部结点。
红黑树具有以下性质:
- 每个结点都是红色的或者是黑色的
- 根结点是黑色的
- 每个叶结点NIL是黑色的
- 如果一个结点是红色的,它的两个子结点都是黑色的
- 每个结点到其他所有后代叶结点的简单路径上,均包含相同数目的黑色结点,这个属性被称为黑高,记作bh(x)
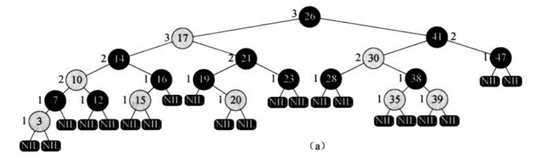
如图是一个红黑树的例子,每个结点边上的数字表示其黑高。每个NIL叶结点都是黑色的。可以使用T.nil哨兵来表示所有的叶结点和根结点的父结点来简化存储,如下图
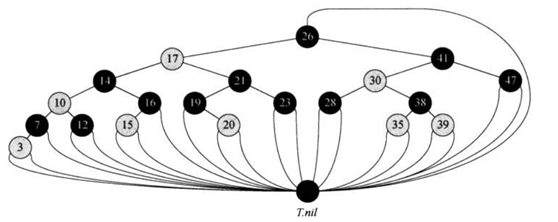
因为通常我们不需要去过多研究NIL结点,所以可以直接省略,集中研究内部结点
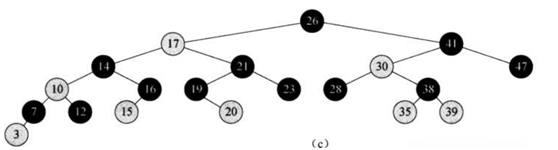
红黑树的黑高定义为根结点的黑高。一棵有n个内部结点的红黑树的高度至多为2lg(n+1),因此SEARCH、MINIMUM、MAXIMUM、SUCCESSOR、PREDECESSOR的操作时间为O(lgn)
旋转
由于TREE-INSERT和TREE-DELETE操作可能会破坏红黑树的性质,因此在这之后需要改变某些结点的颜色和指针结构。修改指针结构的操作就是旋转。

旋转分为左旋和右旋,以左旋为例,y原本是x的右儿子,左旋之后y成为x父亲的新儿子,x成为y的左儿子,y的左儿子成为x的右儿子,也就是从上图的右边变为左边。旋转操作都在O(1)时间内完成,过程中出了指针外其他属性不变。下图展示了用左旋修改一棵树
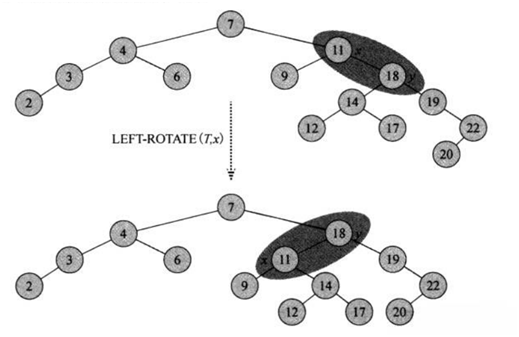
1 LEFT-ROTATE(T,x)
2 y=x.right//y是x的左儿子
3 x.right=y.left//y的左儿子成为x的右儿子
4 if y.left != T.nil
5 y.left.p=x
6 y.p=x.p
7 if x.p == T.nil
8 T.root=y//若x为根则旋转后y为根
9 else if x==x.p.left//否则y成为x父结点的新儿子
10 x.p.left=y
11 else
12 x.p.right=y
13 y.left=x//x成为y的左儿子
14 x.p=y
15
16 RIGHT-ROTATE(T.y)
17 x=y.left//x是y的左儿子
18 y.left=x.right;//x的右儿子成为x的左儿子
19 if x.right != T.nil
20 x.right.p=y
21 x.p=y.p
22 if y.p == T.nil
23 T.root=x//若y为根则旋转后x为根
24 else if y==y.p.left//否则x成为y父结点的新儿子
25 y.p.left=x
26 else
27 y.p.right=x
28 x.right=y//y成为x的右儿子
29 y.p=x
插入
通过RB-INSERT将一个结点像普通二叉树那样插入红黑树并设为红色,然后使用INSERT-FIXUP来对节点重新着色并旋转
1 RB-INSERT(T,z)
2 y=T.nil
3 x=T.root
4 while x!=T.nil
5 y=x
6 if z.key<x.key
7 x=x.left
8 else
9 x=x.right
10 z.p=y
11 if y==T.nil
12 T.root=z
13 else if z.key<y.key
14 y.left=z
15 else
16 y.right=z
17 z.left=T.nil
18 z.right=T.nil
19 z.color=RED
20 RB-INSERT-FIXUP(T,z)
21
22 RB-INSERT-FIXUP(T,z)
23 while z.p.color==RED
24 if z.p==z.p.p.left//若z的父亲是左儿子
25 y=z.p.p.right//y是z的叔叔
26 if y.color==RED//情况1
27 z.p.color=BLACK
28 y.color=BLACK
29 z.p.p.color=RED
30 z=z.p.p
31 else if z==z.p.right//情况2
32 z=z.p
33 LEFT-ROTATE(T,z)
34 z.p.color=BLACK//情况3
35 z.p.p.color=RED
36 RIGHT-ROTATE(T,z.p.p)
37 else//left和right交换其他同上面情况
38 y=z.p.p.left//y是z的叔叔
39 if y.color==RED//情况1
40 z.p.color=BLACK
41 y.color=BLACK
42 z.p.p.color=RED
43 z=z.p.p
44 else if z==z.p.left//情况2
45 z=z.p
46 RIGHT-ROTATE(T,z)
47 z.p.color=BLACK//情况3
48 z.p.p.color=RED
49 LEFT-ROTATE(T,z.p.p)
50 T.root.color=BLACK
先分析一下可能会造成红黑树性质被破坏的情况:
情况1:z的叔结点y是红色的,这种情况下无论z是左儿子还是右儿子都可以只靠染色来维持红黑树性质。
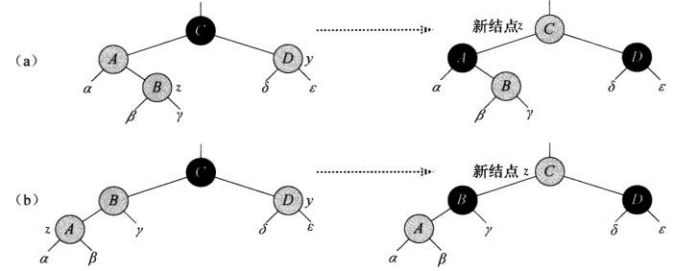
情况2:z的叔结点y是黑色的且z是一个右孩子
情况3:z的叔结点y是黑色的且z是一个左孩子
情况2可以通过左旋转变到情况3,情况3再通过改变某些结点的颜色后进行右旋,保持红黑树的性质
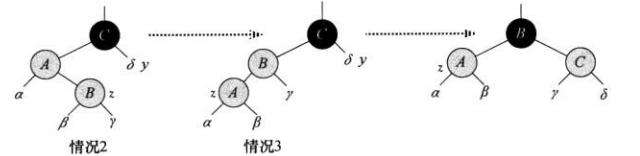
下面是一个完整的操作实例
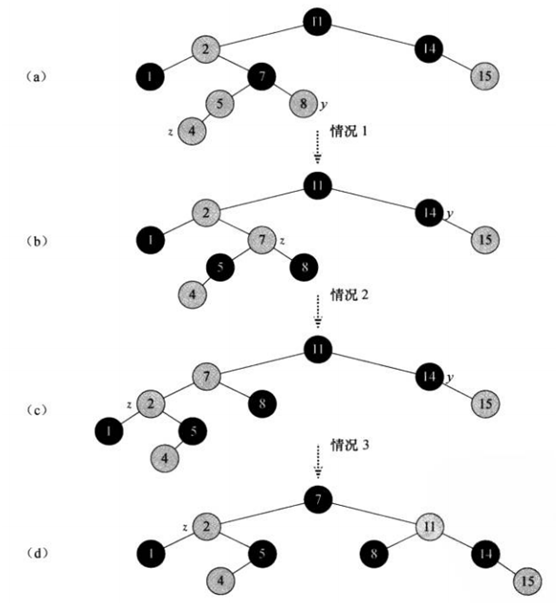
如图z和z的父结点z.p都是红色,且z.p有右兄弟y为红色,属于情况1,将z.p和y都染黑然后z.p.p染红,z指向z.p.p。现在z.p的右兄弟y是黑色的,同时z是右儿子属于情况2,z指向z.p后对z进行左旋。现在z.p有右兄弟y是黑色的,z是左儿子属于情况3,z.p染黑.z.p.p染红然后对z.p.p进行右旋,最后确保根结点是黑色的。
删除
红黑树的结点删除操作同样是基于二叉树删除改造而来,首先是TRANSPLANT方法,这个方法的作用是要删除结点u时把结点v填到u原本的位置。然后就是实际删除操作RB-DELETE, z的子结点少于2个时,删除z结点,子结点取代z的位置。z有两个儿子时,y是右子树中最小的一个作为z的后继,y移动到z的位置,z的左子树移交给y,y.right替换y原本的位置,若y原本是黑色,则需要检查y.right是否破坏了红黑树结构。由于删除后可能会破坏红黑树性质,所以和插入一样也需要执行修复操作
1 RE-TRANSPLANT(T,u,v)
2 if u.p==T.nil
3 T.root=v
4 else if u==u.p.left
5 u.p.left=v
6 else
7 u.p.right=v
8 v.p=u.p//v.p的赋值无条件执行,因为u是root时v.p是T.nil该赋值依然成立
9
10 RB-DELETE(T,z)
11 y=z
12 y-original-color=y.color
13 if z.left=T.nil
14 x=z.right
15 RB-TRANSPLANT(T,z,z.right)//z左儿子不存在则右儿子顶替z
16 else if z.right==T.nil
17 x=z.left
18 RB-TRANSPLANT(T,z,z.left)// z右儿子不存在则左儿子顶替z
19 else
20 y=TREE-MINIMUM(z.right)//y是z的右子树中最小的结点,即除NIL之外最左的结点
21 x=y.right//x是y的右儿子
22 if y.p==z
23 x.p=y//若y的右子树中没有左儿子,x.p=y(本来就是)
24 else
25 RB-TRANSPLANT(T,y,y.right)//用y.right替换y的位置
26 y.right.p=y
27 RB-TRANSPLANT(T,z,y)//用y替换z的位置
28 y.left=z.left//z的左子树移到y的左子树上,y本身没有左子树
29 y.left.p=y
30 y.color=z.color//y的颜色换成z的颜色
31 if y-original-color==BLACK
32 RE-DELETE-FIXUP(T,x)//若y原本是黑色则移走y后原本包含y路径的黑高会改变导致破坏红黑树性质
33
34 RB-DELETE-FIXUP(T,x)
35 while x != T.root and x.color == BLACK
36 if x == x.p.left
37 w=x.p.right//w是x的兄弟
38 if w.color == RED
39 w.color=BLACK//case1
40 x.p.color=RED
41 LEFT-ROTATE(T,x,p)
42 w=x.p.right
43 if w.left.color == BLACK and w.right.color == BLACK
44 w.color=RED//case2
45 x=x.p
46 else if w.right.color == BLACK
47 w.left.color=BLACK//case3
48 w.color=RED
49 RIGHT-ROTATE(T,w)
50 w=x.p.right
51 w.color=x.p.color//case4
52 x.p.color=BLACK
53 w.right.color=BLACK
54 LEFT-ROTATE(T,x,p)
55 x=T.root
56 else(上面的情况交换left right)
57 x.color=BLACK
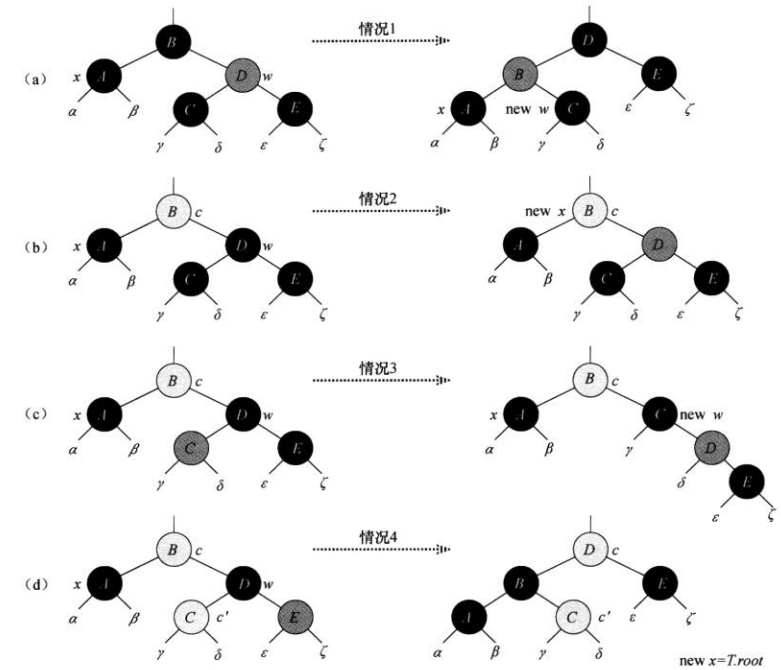
情况1:x的兄弟w是红色的,w一定会有黑色的子结点,改变w和x.p的颜色,然后对x.p进行一次左旋。现在w是原本w的某个子结点,可能转为情况234
情况2:x的兄弟w是黑色的,w的两个子结点都是黑色的。w染红,x上升到x.p,若原本x.p是红色的(从情况1进入情况2就是这样的)则循环结束,将新的x染黑即可。
情况3:x的兄弟w是黑色的,w左儿子红色,右儿子黑色。交换w和w.left的颜色,然后对w进行右旋,这样w有一个红色的右儿子,转入情况4
情况4:x的兄弟结点w是黑色的,且w的右儿子是红色的,左儿子颜色不限。对x.p执行左旋之后,再对部分结点重新染色。